Geometry

The mathematics of lines, shapes, and angles. Essential stuff for describing the world around you.
« Back to dashboard
« Back to dashboard
1. Lines and angles
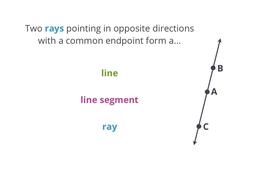
Learn about lines, rays, and line segments
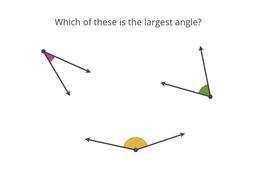
Learn what angles are, and how to measure them
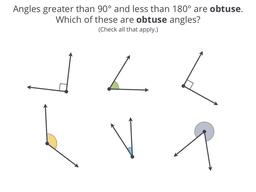
Learn the names for angles of all sizes
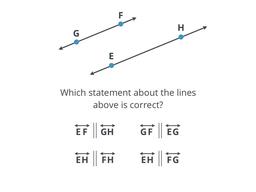
Lines that never, ever cross
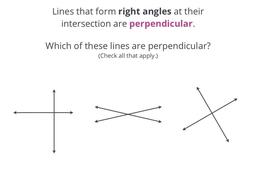
Lines that cross, forming right angles
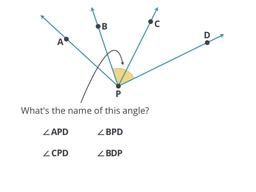
With these rules, you know which angle you mean
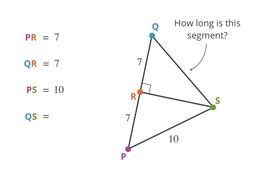
The equidistant points also cut segments in two
2. Related angles
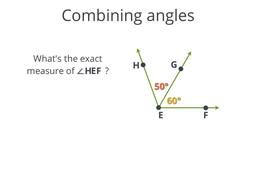
Adding and subtracting adjacent angles
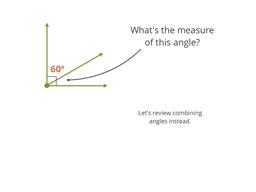
Learn about complementary and supplementary angles

What about angles bigger than 360 degrees?
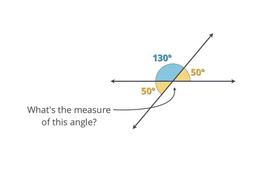
Angles on opposite sides of intersecting lines
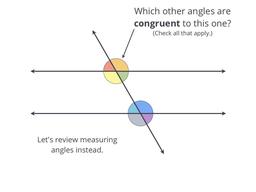
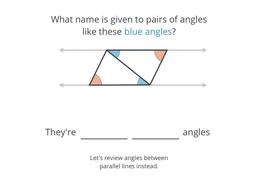
Parallel lines form congruent angles in matching places
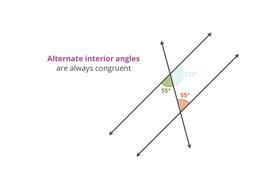
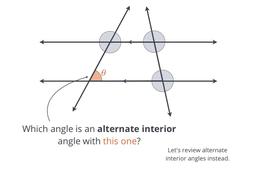
Congruent angles INSIDE parallel lines
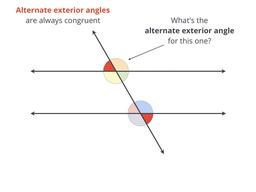
Congruent angles OUTSIDE parallel lines
3. Triangles

A fancy name for shapes with straight sides
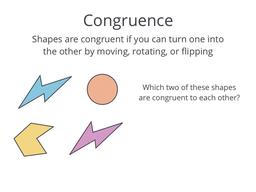
When line segments, angles, or shapes are the same
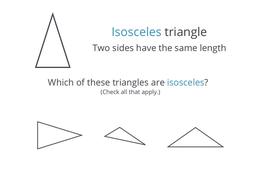
Introducing triangles and three different types of them
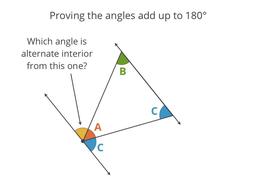
See if it's really true, and then prove it!
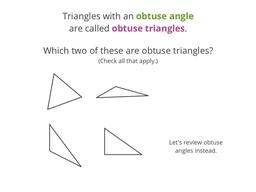
Learn about right, acute, and obtuse triangles
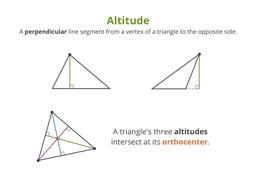
Perpendicular line segments in triangles
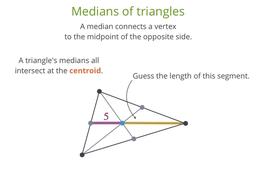
Line segments connecting vertices and midpoints
They have two equal sides, but what about their angles?
The rules a triangle's side lengths always follow
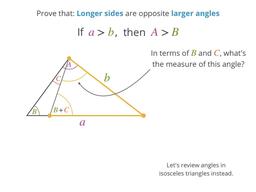
In triangles, sides and their opposite angles are related!
4. Triangle congruence and similarity
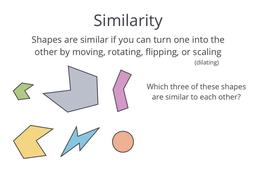
When they have the same shape, but different sizes
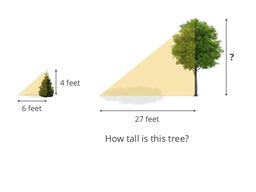
Use similarity to find unknown side lengths!
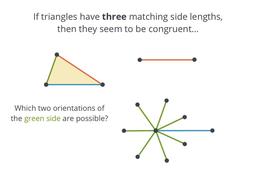
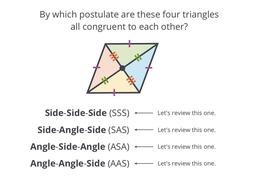
Using sides to see if triangles are congruent
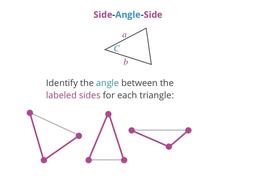
Congruence check using two sides and the angle between
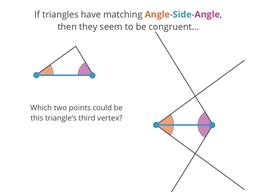
Congruence check using two angles and the side between
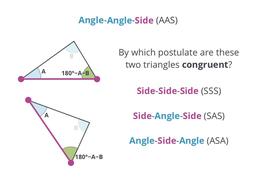
The final congruence check for triangles
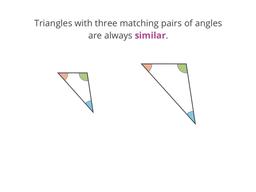
Triangles are similar when they have matching angles
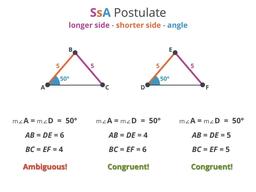
Depending on the sides, you can have 0, 1, or 2 triangles!
5. Polygons and quadrilaterals
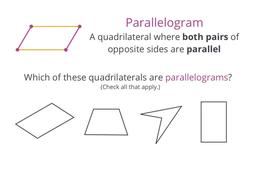
Learn about rectangles, rhombi, and more!

Polygons with equal sides and angles
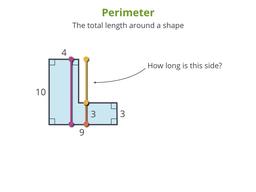
Tricks for finding the distance around a shape
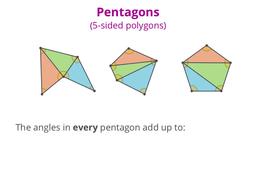
Find a formula for the sum of the angles in any polygon

Opposite angles are congruent in parallelograms
Opposite sides are congruent in parallelograms

In parallelograms, diagonals always bisect each other
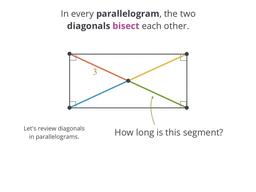
Rectangles always have two congruent diagonals
In rhombi, the diagonals are always perpendicular
Supplementary pairs of angles in trapezoids
6. Area of polygons
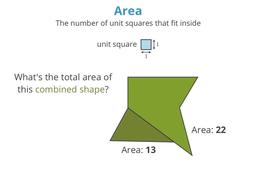
Measuring how much space is inside a shape
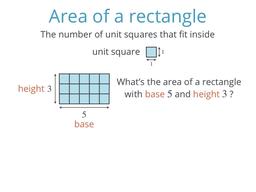
Discover the formula for the area of a rectangle
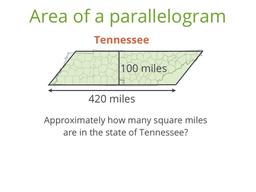
Discover the formula for the area of a parallelogram
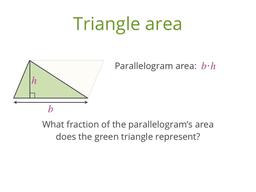
Discover a formula for the area of any triangle
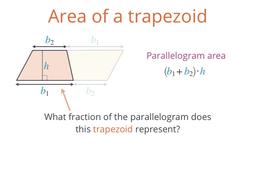
Discover the formula for the area of a trapezoid
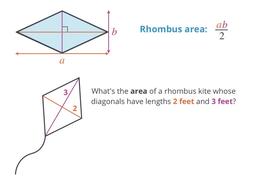
Find a rhombus' area using its diagonals
7. The Pythagorean theorem
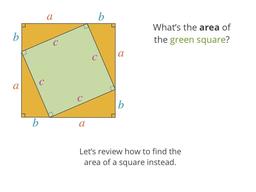
How the sides of right triangles are related
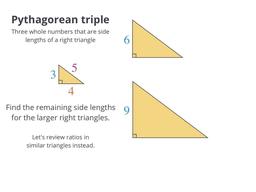
When whole numbers are the sides of right triangles
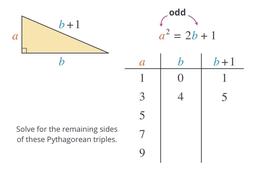
Ways to write out every last Pythagorean triple
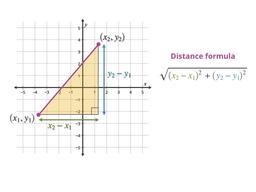
Find the distance between any two points
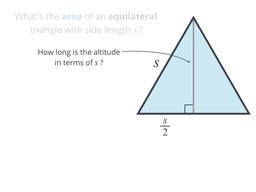
Finding the area of equilateral and isosceles triangles

Another way to find the area of a triangle
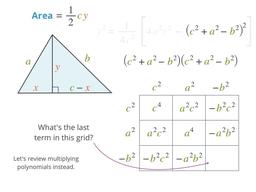
You might know the formula, but where does it come from?
8. Circles, ellipses, and their areas
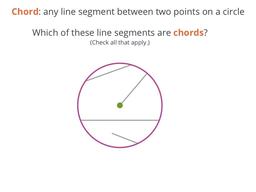
An intro to circles, radii, diameters, and chords

Find the distance around a circle (and then eat some pi)
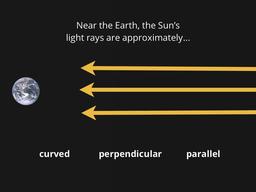
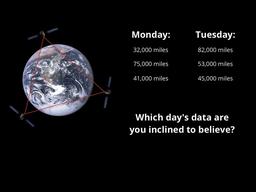
Use shadows to measure the Earth's circumference!
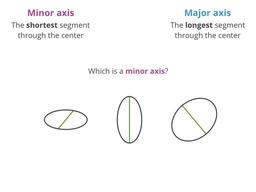
What you get when you "stretch" a circle
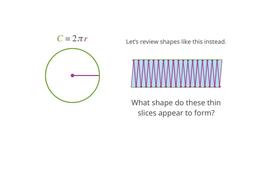
Using circumference to find a circle's area
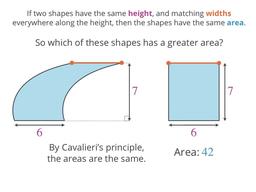
Comparing shapes to find areas of the unusual ones
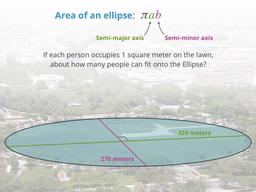
Calculate how many people can fit on the Ellipse in DC
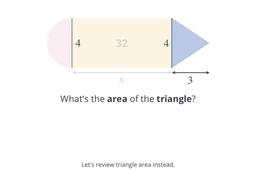
Add and subtract the ares of simpler shapes!
9. Angles in circles
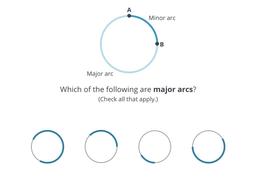
As you'll see, there are 360 degrees in every circle
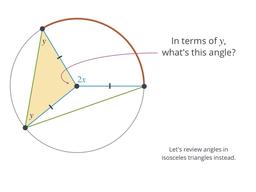
Discover how inscribed angles are related to central angles!
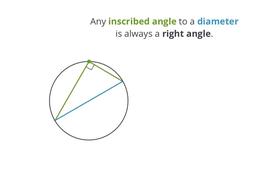
Prove that inscribed angles drawn to diameters are right
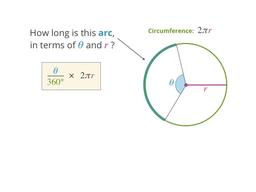
Finding a formula for the length of any arc
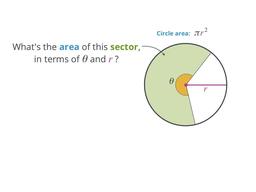
How to find the area of any slice of a circle
10. Lines in circles
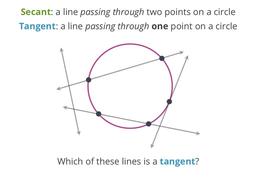
Some lines cross circles twice, others touch them only once
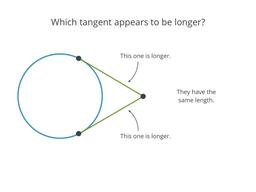
Prove that tangents from the same point are congruent
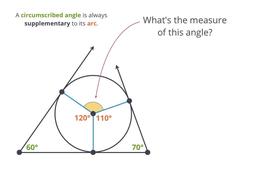
Discover how angles between tangents are related to arcs
Prove that the arcs between them are always congruent
Discover a rule for how intersecting chords relate
See how their opposite angles are related!
Like chords, intersecting secants are also related!
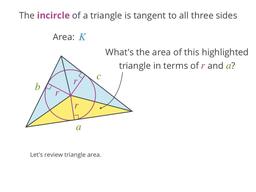
Calculate the radius of any inscribed circle
11. Volume
Learn the names and features of 3D shapes

Discover how to find the volume of any box!

Find the volume of prisms and cylinders

Instead of matching widths, you'll be matching areas!

Starting with a cube, discover the pyramid volume formula

Find the volume of any cone, and learn about slant height
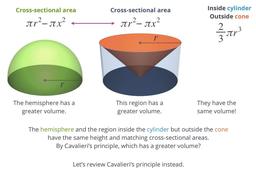
Use Cavalieri's principle to find the volume of a sphere
12. Surface area
Learn why ice is commonly shaped into cubes
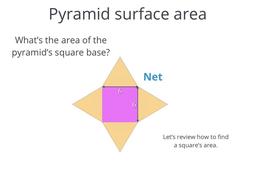
Find a pyramid's surface area using squares and triangles

Unroll any cylinder to find its surface area!

Discover and use the formula for a cone's surface area!
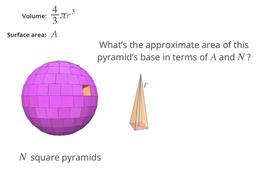
Find the the total area of a sphere's curved surface
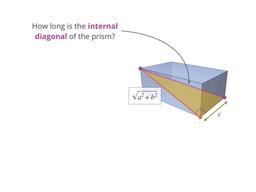
What's the distance between opposite corners of a cube?
13. Transformations
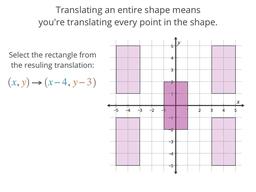
Moving points and shapes in the coordinate plane
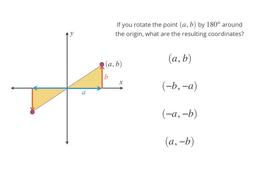
Rotating points and shapes around the origin
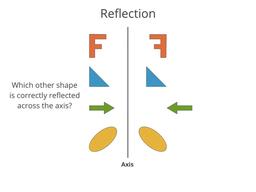
Flipping across different axes (and the origin)
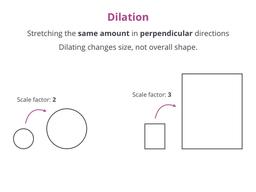
Stretching shapes in one or two directions
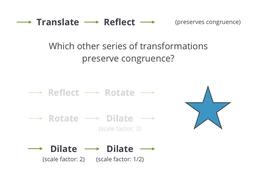
See which transformations keep things congruent

When reflection or rotation doesn't change anything
14. Geometric optics

Using Fermat's principle to understand refraction

Use refraction to understand rainbows and their features

